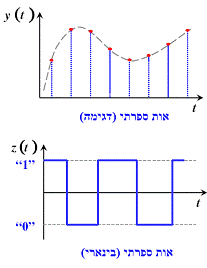
- אותות.
מיון של אותות: אותות אנלוגיים וספרתיים; רציפות בזמן, סינגולאריות, מחזוריות. אותות בסיסיים: אות הרמוני (טון); אות Sin c וגל ריבועי.מאפיינים של אותות: ערך ממוצע (DC), ערך יעיל RMS, הספק, אנרגיה. - אנליזה של אותות במישור תדר:טור Fourier והתמרת Fourier, תכונותיהם.

אשר בתנאיי שאות שעבר במכשיר( מערכת) כל שהא יהיה בגבולות " זמן" t : {∞+≥ t ≥ ∞- }
מיון של אותות
מחזוריות
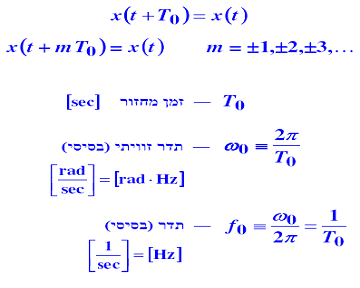
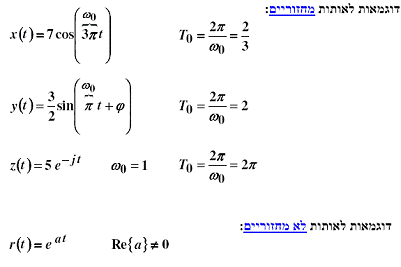
מסקנה : אות ערך קבוע (DC) לא נחשב לאות מחזורי אלה הוא s(t)=const
אות מוגבל בזמן
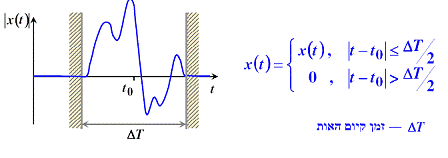
- אותות בסיסיים
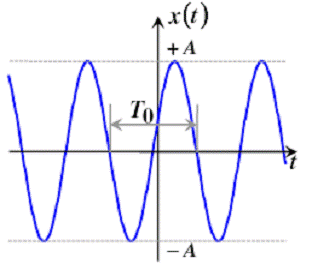
- אות הרמוני (טון הרמוני) Harmonic Signal-

ערך A הוא max האות שיכול להגיע.
גל ריבועי Rectangular wave –

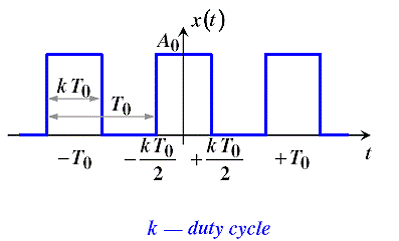
או אות שעון.
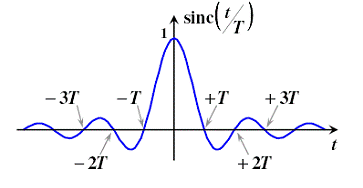
אות Sinc
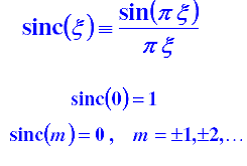
רמת ה-DC של האות
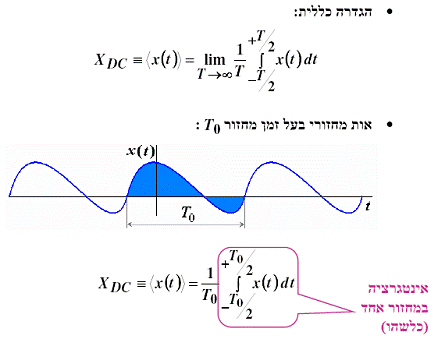
מסקנה – רמת הDC של האות הוא ערך ממוצע האות.
הספק האות Average power –
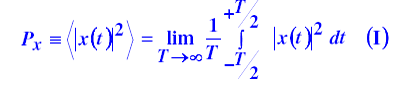
אנרגיה של האות Energy-
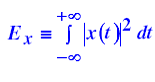
ערך יעיל Rms))-Root Mean Square
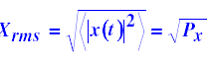
סטיית תקן-Standard deviation

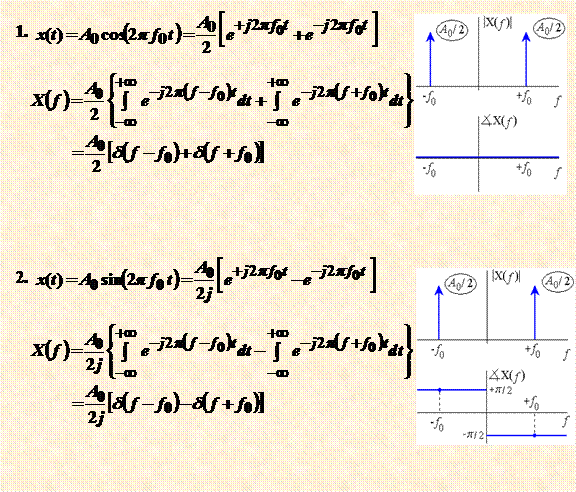
התמרת Fourier
בהגדרת התמרת פורייה שמונח זה מתעסקים עבורו באלקטרוניקה שמתייחסים לאותות הבדידים שהם מוגדרים במישור תדר בלבד אשר נוח לעבודה ולעיבוד האות הרצים לפירוקו לאותות בדידים שמשתנים בתדר,בא לדי ביטוי שמותר לפרק כל אות לטור פורייה פשוט נוח וקל יחסית לרוב האותות האנלוגיים , בסיס אנלוגי עבור הרכב אות מוצא של מכשיר מדידה .
בהגדרת התמרת פורייה שמונח זה מתעסקים עבורו באלקטרוניקה שמתייחסים לאותות הבדידים שהם מוגדרים במישור תדר בלבד אשר נוח לעבודה ולעיבוד האות הרצים לפירוקו לאותות בדידים שמשתנים בתדר,בא לדי ביטוי שמותר לפרק כל אות לטור פורייה פשוט נוח וקל יחסית לרוב האותות האנלוגיים , בסיס אנלוגי עבור הרכב אות מוצא של מכשיר מדידה .
נוסחה כללית:
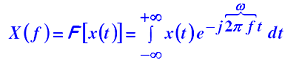
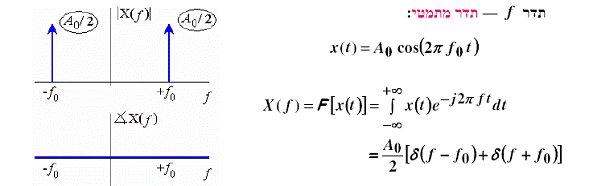
דוגמאות לשימושי Fourier :